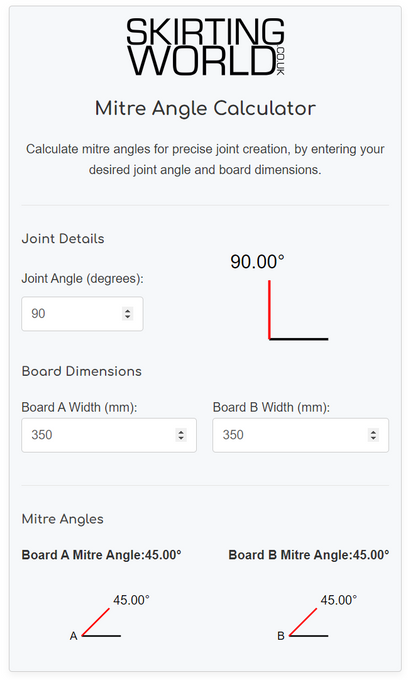
Mitre Angle Calculator | Calculate Miter Angles | Visualiser
Posted by Skirting World on 29th May 2025
How To Use The Mitre Angle Calculator
This calculator helps you find the precise mitre angles for joining two boards at a specific angle. Here's how to use it:
1. Enter the Desired Joint Angle:
- In the "Joint Angle" field, type the angle you want for your finished joint. For example, enter 90° for a square corner, 45° for an octagon, etc.
- Make sure the angle is between 0 and 180 degrees. If your joint is beyond 180°, use the corresponding angle.
2. Enter Board Widths:
- In the "Board A Width" and "Board B Width" fields, type the respective thicknesses of the boards you're joining, and select the correct unit for both entry fields.
3. Review the Results:
- The calculator will display the calculated mitre angle for each board, rounded to two decimal places.
- The "Board A Mitre Angle" and "Board B Mitre Angle" section will display your results in numerical values and visual angle diagrams.
Pro tip: You can verify these figures are correct by simply adding them together. If correct, they will equal the joint angle.
4. Use the Angles for Cutting:
- Transfer the calculated mitre angles (in degrees) to your mitre saw, mitre box, or other cutting tool.
- Set the saw to the respective angles for each board and make your cuts carefully.
Tips:
- Double-check all your inputs before calculating.
- Consider testing the cuts on scrap wood before working on your actual project.
- If you're unsure about using a mitre saw, consult a professional or watch instructional videos.
Additional Notes:
- This calculator functions with any joint angle between 0 - 180 degrees and boards of the same or varying widths.
- The calculator provides visual aids to help understand the angles, but always double-check the numerical values before cutting.
How To Calculate Mitre Angles
To skip the manual calculation and save time, click the button below to jump to the mitre angle calculator.
Calculating mitre angles might seem intimidating, but understanding the basic principles and using the right formulas makes it easier than you think. Let's break it down for the three most common scenarios.
Scenario 1: 90° Joint & Same Width Boards
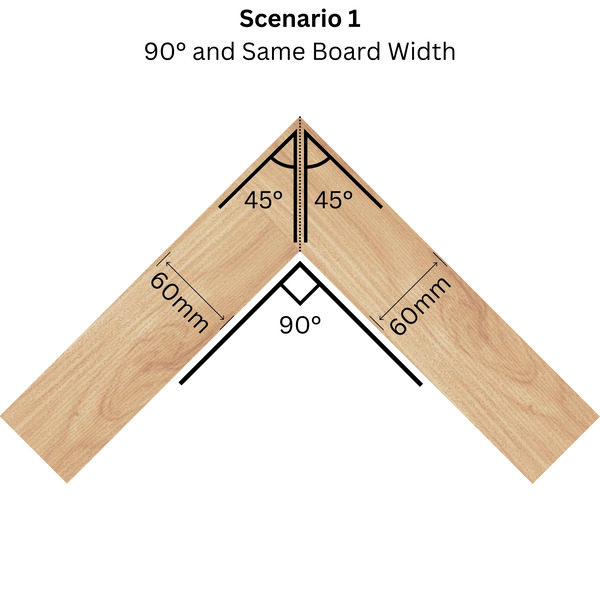
Imagine making a picture frame. Both pieces need angled cuts so they join perfectly at a corner. This is the easiest case:
Formula:
Breakdown: Since you're creating a 90° corner with two pieces, each piece needs a 45° mitre cut (half of the joint angle).
Scenario 2: 90° Joint & Different Width Boards
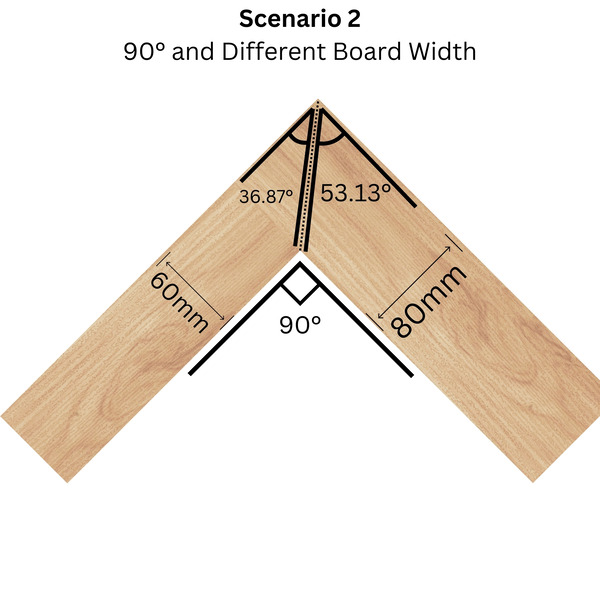
Now, let's say your frame pieces have different widths. Here's where things get a tad trickier:
Formula:
Breakdown: Imagine a seesaw: the narrower board is like the lighter side, needing a steeper angle to balance with the wider board (heavier side).
arctanis a fancy math term that helps find that balance angle.45°represents the "perfect balance" angle for same-width boards. We adjust it based on the board width difference.
Example:
Your narrower board is 60mm, and the wider one is 80mm.
- Wider board: arctan( (80mm / 60mm) * tan(45°) ) ≈ 53.13°
Scenario 3: Any Angle Joint & Same/Different Width Boards
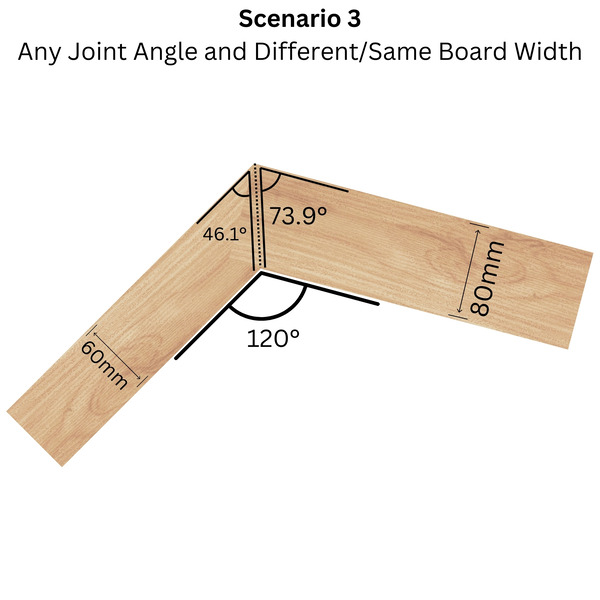
Mitre cuts aren't limited to 90° corners! You can create any angle you desire:
Formula:
Breakdown: The arctan function within the mitre angle formula translates the interplay between board widths, trigonometric functions (sin and cos of the desired joint angle), and a conversion factor, ultimately delivering individual board angles for a precise joint.
Example:
You want a 120° joint with a 60mm board and an 80mm board.
- Wider board: arctan( (80mm * sin(120°)) / (60mm + 80mm * cos(120°)) ) * 180 / π ≈ 73.90°
Remember:
- Measure board widths accurately! Even a small mistake can throw off your cuts.
- Double-check your calculations before sawing. There's no undo button in woodworking!
- Online calculators can be helpful for quick angle checks, but understanding the formulas gives you flexibility.
What Is A Mitre Saw?
A mitre / miter saw, also known as a drop saw, is a powerful tool specifically designed for making precise angled cuts in wood and other materials. It's an indispensable tool for many woodworking projects, especially those involving joining pieces at angles, such as picture frames, crown moulding, and even complex joinery.

How Mitre Saws Work
Unlike a circular saw that spins its blade against the material, a miter saw features a stationary blade mounted on an arm. This arm can be pivoted horizontally (mitre angle) and vertically (bevel angle) to achieve your desired cutting angle. The workpiece itself rests on a flat table and feeds against the fixed blade. This controlled approach offers cleaner, more accurate cuts compared to freehand sawing.
How To Use A Mitre Saw
1. Setting the Angles:
Before cutting, adjust the miter and bevel angles according to your project's requirements. Most mitre saws have easy-to-read scales on both axes to set the desired angles precisely.
2. Making the Cut:
Secure your workpiece firmly on the table, ensuring it stays flat and aligns with the saw blade. Once everything is set, carefully lower the saw arm through the material, making a clean and accurate cut at the chosen angle.
Finding the Complementary Angle:
Mitre saws are most commonly set at an angle of 0°, this cuts along the board at an angle of 90°. To find the complementary angle on the mitre saw for your mitre angles, use the following formula:
Mitre Box
A mitre box is a much simpler and easier tool to use than a mitre saw, however they are usually restricted to a small range of angles. For more precise cuts, you would need to use a mitre saw or make manual markings.
What Is A Mitre Cut?
Instead of a straight cut, a mitre cut is an angled one made across the width of your board. You'll most often see them at 45 degrees, but they can be any angle depending on your project. Think of it like a special angled joint, like the perfect corner of a picture frame.
Why Use Mitre Cuts?
- Clean corners: Mitre cuts create sharp, seamless joints that look professional, whether you're making picture frames, moulding, skirting boards, architraves or other projects.
- Stronger joints: Done right, mitre joints can be stronger than simply butting two pieces together, giving your project extra durability.
Things to remember:
- Width, not length: Mitre cuts are made across the width of the board, not the length.
- Get the angle right: The correct angle is crucial for a perfect fit. You can use specialised tools like mitre saws for precise cuts, or calculate the angle yourself.
- Beyond 45 degrees: Not every corner needs to be a 90-degree angle. Mitre cuts can be any angle you need, depending on your project design.
Where Are Mitre Cuts Used?
Interior Trims
- Skirting boards: Mitre cuts ensure seamless transitions at corners, contributing to a polished and unified appearance.
- Wall panels: Whether wood, MDF, or other materials, mitre cuts create professional-looking joints at internal and external corners.
- Architraves and door/window casings: Framing with mitred casings adds refinement and strengthens the joints for improved durability.
- Ceiling and cornice mouldings: Achieving flawless transitions in these decorative elements relies heavily on precise mitre cuts.
Furniture Construction
- Box joints: Mitre cuts create sharp and strong corners in tabletops, drawer sides, and cabinet doors, enhancing both aesthetics and functionality.
- Angled legs and supports: Tables, chairs, and other furniture with angled legs often require mitre cuts for stable and visually appealing connections.
- Decorative elements: Adding trim, edging, or other decorative details to furniture frequently involves mitre cuts for precise corner detailing.
Other Applications
- Custom shelves and built-ins: Both straight and angled shelves and built-ins often utilise mitre cuts for professional-looking corners and precise joints.
- Angled boxes and planters: Creative designs like hexagonal planters or triangular boxes are made possible with mitre cuts, adding a unique touch to various projects.
- Geometric woodworking projects: From stars and snowflakes to complex patterns, mitre cuts unlock endless possibilities for incorporating geometric elements into wall art, decorative pieces, or furniture accents.









